[Quantum Information] Evolution

 Evolution

Notes from RWTH Aachen University course 
“Quantum Information” Summer semester 2020
professor: Wegewijs, Maarten

Evolution 

• probability should stay probability $\Rightarrow\mathcal{E}$ is a stochastic map.

• Positivity Preservation (PP): $\mathcal{E}(\rho)\geq 0$

• Trace Preservation (TP): $\text{tr }\mathcal{E}(\rho)=1$

• 🧐 These are general restrictions for quantum evolutions?

  • ❌ Difficult in principle: because of entanglement
  • ❌ Difficult in practice: PP is more complicated than complete positivity

⭐️⭐️⭐️ Evolutions (superoperators) correspond to states (operators)
$\rho'=$$\sum_m M_m$$\rho$$M_m^\dagger$ $\longleftrightarrow$ $\sum_m|M_m\rangle\langle M_m|$
We take maximally entangled pure state  $$\frac{1}{\sqrt{d}}|\mathbb{1}_{AB}\rangle=\frac{1}{\sqrt{d}}\sum_i|i_A\rangle\otimes|i_B\rangle$$
$\sigma_{AB}$$=($$\mathcal{E}_A$$\otimes\mathcal{I}_B)$$\frac{1}{d}|\mathbb{1}_{AB}\rangle\langle\mathbb{1}_{AB}|$
$$\sigma_{AB}\xleftarrow{one-}\xrightarrow{to-one}\mathcal{E}_A$$
example:
$\mathcal{E}_A$$=\lambda_0\mathbb{1}_A\bullet\mathbb{1}_A+\lambda_1 Z_A\bullet Z_A$
$\sigma_{AB}$$=$$\frac{1}{2}$$\lambda_0|\mathbb{1}_{AB}\rangle\langle \mathbb{1}_{AB}|+\lambda_1 |Z_{AB}\rangle\langle Z_{AB}|$

• Finite-time evolution
  $$U(t) = e^{-iHt} \\ H: \text{Hamiltonian},\ H^\dagger = H \\ H \text{ and } H+\varphi \text{ describes the same evolution for any } \varphi \in \mathbb{R}$$

Evolution in presence of entanglement: Quantum Channels

1. Linear map
2. Hermicity-preserving map (HP): $\rho_A=\rho_A^\dagger\Rightarrow\mathcal{E}_A(\rho_A)=(\mathcal{E}_A(\rho_A))^\dagger$
3. Completely-positive map(CP): $\rho_{AB}\geq 0\Rightarrow \mathcal{E}_A\otimes\mathcal{I}_B(\rho_{AB})\geq 0$

   $\Rightarrow$ PP $\Rightarrow$ HP

4. Trace-preserving map(TP): $\text{tr }\mathcal{E}(\rho)=\text{tr }\rho=1$

• Complete positivity preservation: How is the input state prepared?
• Any mixed input state on A ultimately arises from entanglement with some preparation system B:

• A superoperator $\mathcal{E}_A$ is called completely positive (CP) when it preserves positivity even when extended to act "trivially" on any preparation ancilla B in any joint state
  $$\rho_{AB}\geq 0 \Rightarrow \mathcal{E}_A\mathcal{I}_B(\rho_{AB})\geq 0$$

$$PP\neq CP$$

• PP-non-CP: negative probabilities
  • example: transposition superoperator $\mathcal{E}_A(\rho_A)=\rho_A^{T_A}$

⭐️⭐️⭐️ The difference between PP and CP constitudes what is quantum about evolution: Entanglement

Measurement model for evolution

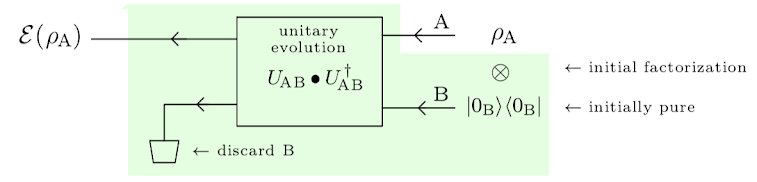
• 🧐 What state-evolutions can we get by coupling to an inaccessible system (B) in a pure state?
• $$\rho_A'=\mathcal{E}_A(\rho_A)=\text{tr}_B\{{U_{AB}(\rho_A\otimes |0_B\rangle\langle 0_B|)U_{AB}^\dagger}\}$$
• 🧐 What state-evolutions can we get by coupling to an extra system (B) in a pure state, measuring it, and discarding the complete outcomes?
• Projective measurement $\{\mathbb{1}_A\otimes|b_B\rangle\langle b_B|\}$ in B-basis $|b_B\rangle$
  
• Discarding complete outcome b

• $$\mathcal{E}_A(\rho_A)=\sum_b p_b\rho_{Ab}=\sum_bM_{Ab}\rho_AM_{Ab}^\dagger$$

• 🧐 Are evolutions derived from measurement models indeed CP-TP maps?

  • ⭕️

• 🧐 Does every operator-sum evolution $\mathcal{E}_A$ correspond to a unique model $\{U_{AB},|0_B\rangle\}$?

• ❌
• Nonuniqueness comes from
• $\langle b_B|$ $U_{AB}|c_B\rangle$
• $M_{Ab}=\sum_{b'}$$\langle b_B|b_B'\rangle$$M_{Ab}'$

• 🧐 Given any CP-TP map $\mathcal{E}$ how to compute a set of measurement operators $\{M_k\}$?

  1. compute a bipartite state corresponding to $\mathcal{E}$  $$\sigma_{AB}=(\mathcal{E}_A\otimes\mathcal{I}_B)\frac{1}{d}|\mathbb{1}_{AB}\rangle\langle\mathbb{1}_{AB}|$$
  2. Diagonalize it  $$\frac{1}{d}\sum_k|(M_k)_{AB}\rangle\langle (M_k)_{AB}|$$
  3. write down operator sum with operators $M_k$  $$\mathcal{E}=\sum_kM_k\bullet M_k^\dagger$$

These are called canonical measurement operator.

Purification of evolution = tomography+purification
$$\frac{1}{d}\mathbb{1}_A=\text{tr}_C\frac{1}{d}|\mathbb{1}_{AC}\rangle\langle\mathbb{1}_{AC}|$$

Readings

Nielsen and Chuang

 8.2 Quantum operations

 8.3 Examples of quantum noise and quantum operations

Preskill

 3.2 Quantum channels

 3.3 State-channel duality and the dilation of a channel

 3.4 Three quantum channels

Wilde (advanced)

 4.4 Quantum Evolutions

 4.5 Interpretations of Quantum Channels