[Quantum Information] POVM measurements
POVM measurements
Notes from RWTH Aachen University course
“Quantum Information” Summer semester 2020
professor: Wegewijs, Maarten
POVM
- Effect operator \(E_m\) discribes outcome of measurements without only neccesary restrictions \[E_m\geq 0\ \Leftrightarrow\ p_m\geq 0\\\sum_m E_m=1\ \Leftrightarrow\ \sum_mp_m=1\]
- Effect operator \(E_m\): care about outcome \(p_m\)
- Measurement operator \(M_m\): care about state \(|\psi_m\rangle\)
Effect operator \(E_m\)
- \(\Leftrightarrow\) Positivity \(\langle\psi|E_m|\psi\rangle\geq 0,\ \forall\ |\psi\rangle\)
- \(\Leftrightarrow\) Sumrule \(\sum_m E_m=\mathbb{1}\)
Measurement operator \(M_{Ab}\)
- operators on \(A\):\[M_{Ab}=\langle b_B|U_{AB}|0_B\rangle\]
- post-measurement states on \(A\): \[\rho_{Ab}=\frac{1}{p_b}M_{Ab}\rho_AM_{Ab}^\dagger\]
- The measurement probability \[p_b=\text{tr}_A(M_{Ab}\rho_AM_{Ab}^\dagger)=\text{tr}_A(M_{Ab}^\dagger M_{Ab}\rho_A)\]
where \[E_{Ab}=M_{Ab}^\dagger M_{Ab}\]
⭐️⭐️⭐️ A set of \(\{E_{Ab}\}\) is called a POVM for system \(A\) if \[E_{Ab}\geq 0\\ \sum_b E_{Ab}=\mathbb{1}_A\]
⭐️⭐️⭐️ A set of measurement operators \(\{M_{Ab}\}\) is called a POVM-measurement if \[\sum_b M_{Ab}^\dagger M_{Ab} = \mathbb{1}_A\]
\(E_{Ab}\) and \(M_{Ab}\) are not uniquely corresponding. \[M_{Ab}=V_{Ab}\sqrt{E_{Ab}}\]
🧐 Does a POVM-measurement \(\{M_{Ab}\}\) discribe a posterior states of general measurement?
- ❌ A POVM-measurement is constrained to preserve purity.
- It cannot describe decoherence of pure state to mixed post-measurement state.
🧐 Does every POVM-measurement \(\{M_{Ab}\}\) derive from a pure, complete-measurement model \((U_{AB},|0_B\rangle)\)?
- ⭕️ \[M_{Ab}=\langle b_B|U_{AB}|0_B\rangle \Leftrightarrow U_{AB}=\sum_b M_{Ab}|b_B\rangle\langle 0_B|+...\]
Nonuniqueness comes from
- \(\langle b_B|\) \(U_{AB}|c_B\rangle\)
- \(M_{Ab}=\)\(V_{Ab}\)\(\sqrt{E_{Ab}}\)
Example:
 \[U_{AB}=|0_A\rangle\langle 0_A|\otimes e^{-itX_B}+|1_A\rangle\langle 1_A|\otimes e^{itX_B}\]
\[U_{AB}=|0_A\rangle\langle 0_A|\otimes e^{-itX_B}+|1_A\rangle\langle 1_A|\otimes e^{itX_B}\]- POVM-measurement operator: non-projective
\[M_{A0}=\langle 0_B|U_{AB}|0_B\rangle=\sqrt{\lambda_0}\mathbb{I}_A\neq (M_{A0})^2\] - POVE effects: non-informative \[E_{A0}=\lambda_0\mathbb{I}_A\leftarrow\text{ independent of }\rho_A\]
- POVM-measurement operator: non-projective
 \[U_{AB}=|0_A\rangle\langle 0_A|\otimes \mathbb{I}_B+|1_A\rangle\langle 1_A|\otimes e^{itY_B}\]
\[U_{AB}=|0_A\rangle\langle 0_A|\otimes \mathbb{I}_B+|1_A\rangle\langle 1_A|\otimes e^{itY_B}\]- POVM-measurement operator: non-projective
\[M_{A0}=|0_A\rangle\langle 0_A|+\sqrt{\mu_0}|1_A\rangle\langle 1_A|\neq (M_{A0})^2\] - POVE effects: informative \[E_{A0}=|0_A\rangle\langle 0_A|+\mu_0|1_A\rangle\langle 1_A|\\p_{A0}=\langle 0_A|\rho_A|0_A\rangle+\mu_0\langle 1_A|\rho_A|1_A\rangle\\ \text{probability depends of }\rho_A\Rightarrow\text{ informative}\]
- Example of POVM improvement:
- \(p_\text{certain}=\frac{1}{2}\varepsilon = 0.293\)
\(17\%\) better than projective measurement
⭐️⭐️⭐️ Optimized POVM has better certainty than projective measurement!
i.e. more probability to measure with certainty (100%)
- Pretty good measurement (PGM)
- Ensemble \(\{p_i\rho_i\}\) with full-rank marginal state \(\rho=\sum_i p_i\rho_i\) (all eigenvalues \(\geq0\) ) has a canonical POVM called square-root measurement, or Pretty good measurement \[E_i=\frac{1}{\sqrt{\rho}}p_i\rho_i\frac{1}{\sqrt{\rho}}\]
⭐️⭐️⭐️ Pretty good measurement: Optimized probability of detecting unknown state
POVM: detecting known state
- 🧐 Can evolution in presence of coupling/correlation to an observed environment be reversed? i.e. \(\mathcal{D}\)\(\mathcal{E}\)\((\rho)\stackrel{?}{=}\rho,\ \forall\ \rho\)
- ❌ No information without disturbance.


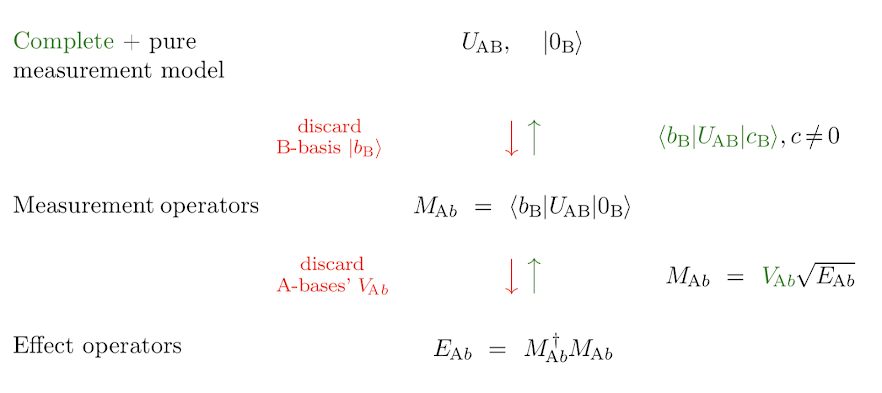


留言
張貼留言